Application of the EEMD and CEEMDAN algorithm for non- linear signal processing

claude mukaz; Moise NGOYI

Authors

claude mukaz ok https://orcid.org/0009-0007-8402-880X
Moise NGOYI KASANJI High Institute of Applied Techniques https://orcid.org/0009-0007-8402-880X

Keywords:

EEMD, CEEMDAN, Non-linear, Algorithm

Abstract

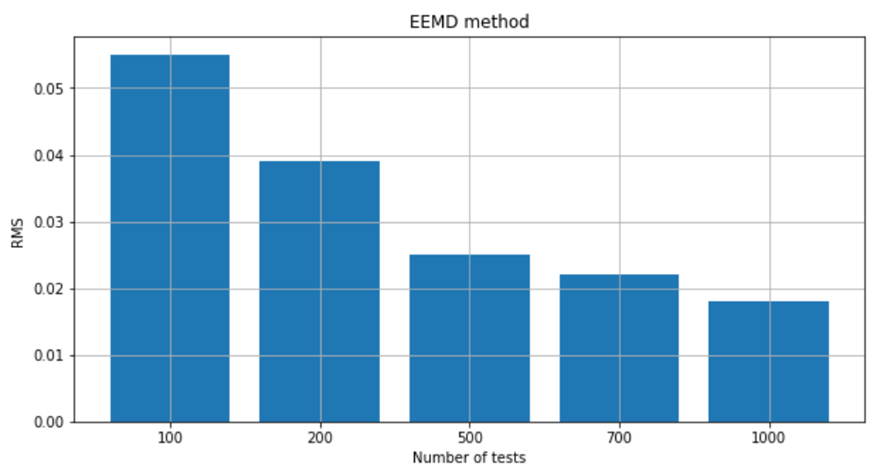
Nonlinear signals are often encountered in many applications, such as biomedical signal processing, fault diagnosis, and image processing. Ensemble empirical mode decomposition (EEMD) and complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) algorithms have been proposed for the analysis of nonlinear and non-stationary signals. In this paper, we compare the performance of EEMD and CEEMDAN algorithms based on the Root Mean Square (RMS) statistical indicator for nonlinear signal processing. We evaluate the effectiveness of these algorithms using two synthetic signals and a real-world vibration signal from a gearbox. The results show that CEEMDAN provides a 50% improvement over EEMD in terms of RMS and the number of trials or computation time required. The study also shows that EEMD is prone to mode mixing and requires a large number of trials to achieve accurate results. On the other hand, CEEMDAN overcomes the mode mixing issue and provides more accurate results with fewer trials or computation time. Our findings suggest that CEEMDAN is a more efficient algorithm for nonlinear signal processing, particularly in real-world applications where computation time is a limiting factor.

Downloads

Download data is not yet available.

Author Biography

Moise NGOYI KASANJI, High Institute of Applied Techniques

ok

References

H. Mahgoun, "Non-stationary analysis of vibration signals in machine monitoring and failure prevention" PhD thesis, University Ferhat Abbas Setif1, 2013.

E.H. El Bouchikhi, V. Choqueuse, M. Benbouzid, J.F. Charpentier, "Etude Comparative Study of Non-Stationary Signal Processing Techniques Dedicated to the Diagnosis of Asynchronous Generators in Offshore Wind and Tidal Turbines" University of Brest France, 2011.

Huang, N. E., & Wu, Z. (2008). A review on Hilbert-Huang transform: method and its applications to geophysical studies. Reviews of Geophysics, 46(2), RG2006.

D. Duhamel, "Signal Analysis", School of Engineering, France, 2013.

Rilling, G., & Flandrin, P. (2008). One or two frequencies? The empirical mode decomposition answers. IEEE Transactions on Signal Processing, 56(1), 85-95.

Xu, W., & Yu, H. (2016). A review of ensemble empirical mode decomposition: algorithms, principles, and applications. Signal Processing, 134, 167-178.

Li, X., Li, H., Li, S., & Liu, Z. (2019). A novel adaptive decomposition method based on complementary ensemble empirical mode decomposition with adaptive noise. Applied Sciences, 9(10), 2102.

J. D. Zheng, J. S. Cheng, Y. Yang, “Partly ensemble empirical mode decomposition: an improved noise-assisted method for eliminating mode mixing,” Sign. Process. 96, 362–374, 2014.

Wu, Z., & Huang, N. E. (2009). Ensemble empirical mode decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis, 1(1), 1-41.

Li, X., Li, H., Li, S., & Liu, Z. (2019). Improved complementary ensemble empirical mode decomposition with adaptive noise for fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing, 116, 791-807.

J. R. Yeh, J. S. Shieh, “Complementary ensemble empirical mode decomposition a novel noise enhanced data analysis method,” Adv. Adapt. Data Anal., vol. 2 (2), 135–156, 2010.

Huang, N. E., & Wu, Z. (2008). A review on Hilbert-Huang transform: method and its applications to geophysical studies. Reviews of Geophysics, 46(2), RG2006.

W. Mohguen, "Improvements of the EEMD method" Magister's thesis, Université Setif-1, 2014.

G. Rilling, "Empirical Modal Decomposition - Contributions to the theory, algorithm and performance analysis" PhD thesis, University Lyon-Ecole Normale Supérieure de Lyon, 2007.

Numes J. C., Deléchelle E., Empirical mode decomposition: Application on signal and

image processing. Advances in Adaptive Data Analysis., 1(1):125–175, 2009.

Torres, M. E., Colominas, M. A., Schlotthauer, G. and Flandrin P., A Complete Ensemble Empirical Mode Decomposition with Adaptative Noise. IEEE Ann. Int. Conf.on acoustics, Speech and Signal Processing ICASSP’11., 4144-4147, 2011.

Torres M.E., Colominas M.A., Schlotthauer G., Flandrin P. (2011) A complete ensemble empirical mode decomposition with adaptive noise, in: Proceedings of the 36th IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), IEEE, pp. 4144–4147.

J.C. Cexus, "Analysis of non-stationary signals by Huang transform, Teager-Kaiser operator and Huang-Teager transform (THT)" PhD thesis, University of Rennes1, 2005.

Salisbury J. I., Sun Y., Rapid screening test for sleep apnea using a nonlinear and non stationary signal processing technique. Med. Eng. Phys., 29 (3): 336–343, 2007.

Hochreiter S., Schmidhuber J. (1997) Long short-term memory, Neural Comput. 9, 8, 1735–1780.

Salisbury J. I., Sun Y., Rapid screening test for sleep apnea using a nonlinear and non stationary signal processing technique. Med. Eng. Phys., 29 (3): 336–343, 2007.

Torres M.E., Colominas M.A., Schlotthauer G., Flandrin P. (2011) A complete ensemble empirical mode decomposition with adaptive noise, in: Proceedings of the 36th IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), IEEE, pp. 4144–4147.

Torres, M. E., Colominas, M. A., Schlotthauer, G. and Flandrin P., A Complete Ensemble Empirical Mode Decomposition with Adaptative Noise. IEEE Ann. Int. Conf.on acoustics, Speech and Signal Processing ICASSP’11., 4144-4147, 2011.

Huang N. E., Yeh J. R., and Shieh J. S., Complementary ensemble empirical mode decomposition a novel noise enhanced data analysis method, Advances in Adaptive Data Analysis., Vol. 2, No. 2, 135–156, 2010.

Flandrin P., Rilling G., et Gonçalvès P., Empirical mode decomposition as a filter bank. IEEE Signal Processing Letters., 11(2):112–114, 2004.

Rilling G., Flandrin P., et Goncalvès P., On empirical mode decomposition and its algorithms. In IEEE-EURASIP, Workshop on Non linear Signal and Image Processing, NSIP ’03, Grado (I), juin 2003.